“多即不同” ——衍生现象与强关联物理学

1. 早期固体物理研究范式

自1924年起，由薛定谔，海森堡，泡利，狄拉克等一众科学家建立起的量子理论已经可以解释诸多分子原子级别的物理现象和问题，比如薛定谔在提出薛定谔方程时做的对氢原子的解，它可以准确描述氢原子的能级和跃迁。在微扰论的意义上，对于诸如氦原子之类的原子核核子质量较大的原子也可以进行一定的解释。于是物理学家们便如同20世纪初那般认为物理学的大厦再一次被建立了起来，剩下的事情都是解一解方程。同一时刻，由于实验技术的发展（如X射线探测技术等），自然而然地，物理学家们会想去用量子理论解释固体中发生的物理现象，如固体材料的电阻，比热等等。

然而，利用量子理论计算固体材料中的物理现象绝非易事，首先，囿于薛定谔方程的特殊性，即使是只考虑自旋自由度的电子系统，在实际材料中的方程自由度也会高达个，这是几乎不可能求解出结果的问题。于是如何利用近似理论从实际材料中提取有效信息便成为了物理学家们所研究的对象之一。

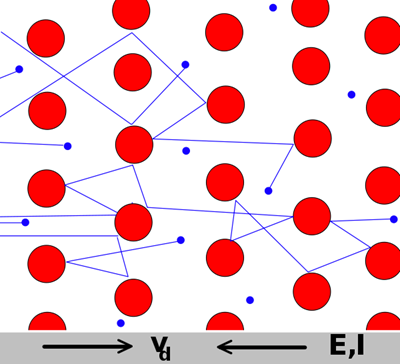
 图1:Drude模型（图中蓝色为电子），图源Wikipedia

1900年左右（这几乎和普朗克提出量子的概念同时），德国物理学家，光学家保罗·朱德(Paul Drude)提出了Drude Theory用以解释材料中电子的输运性质，如电阻电导等。他将电子视为会发生随机碰撞的经典粒子，利用牛顿定律成功地导出了欧姆定律，其理论对于大部分固体材料，尤其是金属材料的正确性非常高。这样一个近似到几乎可以说是错误的简单模型居然能够给出正确的物理预言，这不可谓不是一件神奇的事情。直到今天，半导体领域里依然有很多理论带有Drude Theory的影子。

图2: 从左至右依次为Paul Drude，Arnold Sommerfeld和Philip W. Anderson，图源Wikipedia

后来，当大家已经熟稔了电子的统计学，也就是费米—狄拉克统计，一个自然的想法便是引入这些统计概念去研究含有大量电子的材料体系，如金属等。于是在1927年，德国理论物理学家阿诺德·索末菲（Arnold Sommerfeld）基于旧量子论和自由电子的统计学，提出了自由电子模型（索末菲模型），修正了Drude Theory，建立了如费米面等一系列非常经典的物理概念，尤其是它能够非常成功地解释诸如电子比热的温度依赖，电子态密度形状等问题。

进一步地，若将固体材料中的原子背景所提供的势场视为微扰，由此便可以在两种不同的基底——布洛赫基和瓦尼尔基下建立近自由电子近似和紧束缚近似，从而发展出直到今天都在凝聚态物理学和材料科学中广泛使用的物理理论——能带论。

最后，如果结合原子背景的哈密顿量和电子本身的哈密顿量，利用变分法，选取适当的试探波函数，便可以建立所谓的Hartree-Fock理论，进而发展出一整套第一性原理的计算框架。

以上所列举的各式凝聚态物理和材料物理的研究方法，都是获得了极大成功，可以解释众多物理现象的经典理论和方法，然而，因为他们多基于某些近似和假设，往往不为主流的理论物理学家所认可，因此在很长一段时间里，固态物理学都没有作为一个专门的物理学研究方向，而是被当成类似于应用物理学一样的学科看待。

2. 安德森和他的“多即不同”

上述所列举的各种方法都有一个共同特点：它们都没有考虑电子和电子间的相互作用，也没有考虑电子和原子间的相互作用，而是将这些相互作用转化成有效势场，再去求解单电子问题，也就是所谓的平均场方法（Mean-Field Method）。很快，人们便意识到了这种方法的局限性。

1950年，日本物理学家朝永振一郎(Shinichiro Tomonaga)提出了后来被称为朝永—拉廷格液体（Tomonaga—Luttinger Liquid）的理论模型[1]，它在诸如一维碳纳米管，低温冷原子体系的研究中都有很多应用。然而，这个模型并不是一个可以被上述方法所求解的模型，我们只能在布里渊区中心附近，利用被称为“玻色化（Bosonization）”的场论技巧求解它。同时，人们对于高温超导体，如铜氧化物，和磁性现象，如莫特（Mott）绝缘体的研究让大家意识到，仅仅只是考虑单电子的物理，往往不能够完美解决这些复杂体系的问题。

1972年，凝聚态理论物理学家菲利普·安德森(Philip Anderson)撰写了一篇题为“More is different（多即不同）”的文章[2]，详细阐释了他对于衍生论（Emergent Theory，一译层展论）的理解。他在文中表达了“不同的能标对应不同的物理定律，只知道基本的方程和组成单元并不能够推演出整个宇宙”的核心观点。这宣告了凝聚态物理学的正式诞生，同时也打破了主流（粒子）理论物理学家们一直以来坚信的还原论的观点。

现在回过头来再看之前介绍的那些模型，其实都可以视为固体材料在不同的能标和环境下涌现（emerge）出不同的有效模型。比如Drude Theory可以被认为是固体材料中的电子极度稀薄，平均自由程极大，原子势背景很小。能带论和第一性原理可以计算的材料则对应了平均场可以描述的体系，它们的电子间相互作用涨落不大，相互作用本身可以被有效势场所代替（这与列夫·朗道（Landau）的费米液体理论也相关，这里不多赘述）。而最后，那些电子间相互作用不可以被忽略的体系，便是至今仍留下许多未解之谜，亟待人们去开垦的凝聚态物理学的荒地——强关联体系。

3. 强关联物理和衍生现象

所谓强关联电子体系，是指电子之间的关联（相互作用）很强的体系，这里“很强”本质上是个相对概念，它是指电子间相互作用的能量和电子的动能差不多在一个量级或者远大于电子的动能。在这一基础上，电子和电子间的相互作用便不可以被忽略。在这一情况下，系统往往会涌现出大量奇异的物理现象，如非常规（unconventional）超导体，量子相变，磁性，多体局域化（Many-Body Localization）等等现象。最常见的一类强关联体系，如莫特绝缘体，往往多出现在d区和f区元素中。这些元素所组成的化合物具有很强的原子背景势场，电子被束缚在原子轨道上无法跃迁，然而在微扰意义上电子的自旋自由度会发生被称为“Superexchange”的物理现象，而其他的电子自由度都是没有意义的。此时描述系统的有效哈密顿量便会从赫伯徳（Hubbard）模型涌现成反铁磁海森堡（Anti-Ferromagnetic Heisenberg）模型：

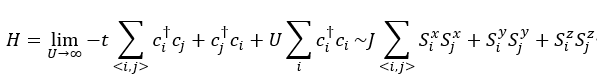
其中第一个等号右边t是跃迁幅度，U是格点上的势能大小，也就是填入一个电子所需要的能量，可以被认为是化学势，c代表费米子的产生湮灭算符。第二个等号右边J代表反铁磁耦合强度，S代表三个泡利矩阵，<i，j>都代表近邻相互作用。

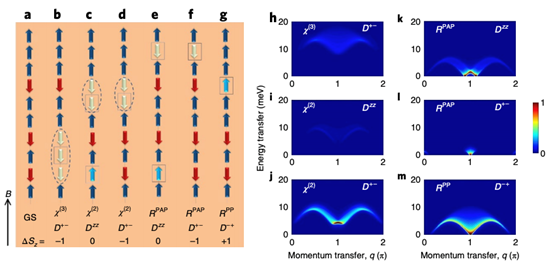
图3: 反铁磁XXZ模型（一类一般性的海森堡模型）的自旋组态和贝特拟设计算出的理论激发谱[3]

海森堡模型是现代凝聚态物理学研究强关联体系和磁性的经典哈密顿量，如何求解海森堡模型也是凝聚态物理学研究中的一大议题。对于一维海森堡模型而言，解析（也就是公式推导）上我们有Bethe-Ansatz（贝特拟设）方法，自旋波（spin wave）方法，玻色化方法，数值上我们有量子蒙特卡洛（Quantum Monte Carlo）方法，密度矩阵重整化群（DMRG）方法。而由于强关联体系的复杂性，二维以上的海森堡模型我们往往只能采用自旋波和蒙特卡洛算法进行求解。

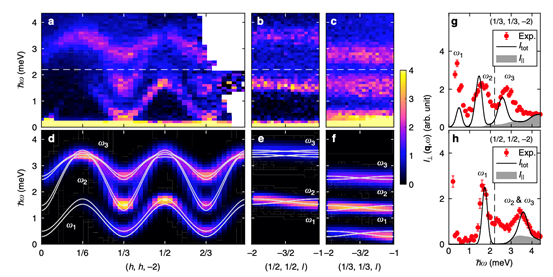
图4: 利用自旋波理论求解的二维海森堡模型的激发（图d,e,f），中子散射对实际海森堡模型描述的材料的测量结果（图a,b,c）[4]

总体而言，强关联体系的研究方法可以大概概括为实验方法，解析方法和数值方法。对于实验而言，大家往往会采用如X射线散射（RIXS），中子散射，核磁共振（NMR）和太赫兹光谱一类的测量手段去探测体系的激发和响应。解析方法则多是场论和重整化群方法。数值上比较常用的便是量子蒙特卡洛，张良网络态方法。

一方面强关联体系蕴含了如此丰富多彩的物理，另一方面由于其体系的复杂性和研究方法的缺失，使得强关联物理学成为自上世纪70年代以来凝聚态物理学研究中的重要组成部分，等待着更多充满天分和热情的青年学者们投入其研究当中。